انتگرالگیری مسیری (Contour integration) فرایندی است که طی آن مقادیر یک انتگرال مسیری حول یک منحنی ساده ی بسته ی فرضی (contour) در صفحه ی مختلط (complex plane) محاسبه می شوند. به عنوان یک نتیجه ی شفت انگیز و جالب توابع هولومورفیک (holomorphic functions)، چنین انتگرال هایی به راحتی می توانند با جمع مقادیر مانده های مختلط (complex residues) داخل منحنی محاسبه شوند.

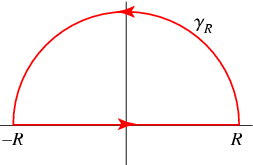
فرض کنیم  و  دو چندجمله ای به ترتیب از درجه ی n و m با ضرایب , ...,  و , ...,  باشند. منحنی بسته ای در نیم صفحه ی بالایی (upper half-plane) همچون شکل بالا داریم. با تعویض x به z، می نویسیم . آنگاه

infty)int_(-R)^R(P(z)dz)/(Q(z)). " src="http://mathworld.wolfram.com/images/equations/ContourIntegration/NumberedEquation1.gif" width=187 border=0>                  

یک مسیر  را که در امتداد محور حقیقی از  تا   مستقیم است، تعریف کرده و یک نیم دایره جهت اتصال دو نقطه ی انتهایی این مسیر مستقیم در نیم صفحه ی مختلط بالایی را رسم می کنیم. به کمک قضیه مانده ها (residue theorem) خواهیم داشت

infty)int_(gamma_R)(P(z)dz)/(Q(z))" src="http://mathworld.wolfram.com/images/equations/ContourIntegration/Inline15.gif" width=93 border=0>    infty)int_(-R)^R(P(z)dz)/(Q(z))+lim_(R->infty)int_0^pi(P(Re^(itheta)))/(Q(Re^(itheta)))iRe^(itheta)dtheta" src="http://mathworld.wolfram.com/images/equations/ContourIntegration/Inline17.gif" width=262 border=0>        

0)Res[(P(z))/(Q(z))]," src="http://mathworld.wolfram.com/images/equations/ContourIntegration/Inline20.gif" width=124 border=0>                                                                            

که   مانده های مختلط (complex residues) را نشان می دهد. با حل

infty)int_(-R)^R(P(z)dz)/(Q(z))=2piisum_(I[z]>0)Res(P(z))/(Q(z))-lim_(R->infty)int_0^pi(P(Re^(itheta)))/(Q(Re^(itheta)))iRe^(itheta)dtheta. " src="http://mathworld.wolfram.com/images/equations/ContourIntegration/NumberedEquation2.gif" width=392 border=0>        

تعریف می کنیم

infty)int_0^pi(P(Re^(itheta)))/(Q(Re^(itheta)))iRe^(itheta)dtheta" src="http://mathworld.wolfram.com/images/equations/ContourIntegration/Inline24.gif" width=153 border=0>               

infty)int_0^pi(b_n(Re^(itheta))^n+b_(n-1)(Re^(itheta))^(n-1)+...+b_0)/(c_m(Re^(itheta))^m+c_(m-1)(Re^(itheta))^(m-1)+...+c_0)iRdtheta" src="http://mathworld.wolfram.com/images/equations/ContourIntegration/Inline27.gif" width=298 border=0>                  

infty)int_0^pi(b_n)/(c_m)(Re^(itheta))^(n-m)iRdtheta" src="http://mathworld.wolfram.com/images/equations/ContourIntegration/Inline32.gif" width=157 border=0>                  

(*)           infty)int_0^pi(b_n)/(c_m)R^(n+1-m)i(e^(itheta))^(n-m)dtheta" src="http://mathworld.wolfram.com/images/equations/ContourIntegration/Inline35.gif" width=176 border=0>                  

و مجموعه ی

آنگاه معادله ی (*)  خواهد شد

infty)i/(R^epsilon)(b_n)/(c_m)int_0^pie^(i(n-m)theta)dtheta. " src="http://mathworld.wolfram.com/images/equations/ContourIntegration/NumberedEquation4.gif" width=178 border=0>            

اینک،

infty)R^(-epsilon)=0 " src="http://mathworld.wolfram.com/images/equations/ContourIntegration/NumberedEquation5.gif" width=70 border=0>                

برای 0" src="http://mathworld.wolfram.com/images/equations/ContourIntegration/Inline36.gif" width=29 border=0>. این بدان معناست که برای =1" src="http://mathworld.wolfram.com/images/equations/ContourIntegration/Inline37.gif" width=86 border=0> و یا  =n+2" src="http://mathworld.wolfram.com/images/equations/ContourIntegration/Inline38.gif" width=55 border=0> ،  داریم

0)Res[(P(z))/(Q(z))] " src="http://mathworld.wolfram.com/images/equations/ContourIntegration/NumberedEquation6.gif" width=209 border=0>         

که در آن =n+2" src="http://mathworld.wolfram.com/images/equations/ContourIntegration/Inline40.gif" width=55 border=0>. در لم گوردن (Jordan"s lemma) تابع مختلط مقدار  را بکار می بریم.  بنابراین بایستی داشته باشیم

infty)f(x)=0, " src="http://mathworld.wolfram.com/images/equations/ContourIntegration/NumberedEquation7.gif" width=78 border=0>              

که برای تصدیق آن باید رابطه ی =n+1" src="http://mathworld.wolfram.com/images/equations/ContourIntegration/Inline42.gif" width=55 border=0> را مطالبه کنیم.

از این رو به ازای =n+1" src="http://mathworld.wolfram.com/images/equations/ContourIntegration/Inline43.gif" width=55 border=0> و 0" src="http://mathworld.wolfram.com/images/equations/ContourIntegration/Inline44.gif" width=30 border=0> داریم:

0)Res[(P(z))/(Q(z))e^(iaz)] " src="http://mathworld.wolfram.com/images/equations/ContourIntegration/NumberedEquation8.gif" width=260 border=0>           

چون این رابطه بایستی به طور جداگانه برای قسمت های حقیقی و مختلط ارضا شود، نتیجه را می توان به دو رابطه ی مهم زیر بسط داد:

0)Res[(P(z))/(Q(z))e^(iaz)]} " src="http://mathworld.wolfram.com/images/equations/ContourIntegration/NumberedEquation9.gif" width=304 border=0>         

0)Res[(P(z))/(Q(z))e^(iaz)]}. " src="http://mathworld.wolfram.com/images/equations/ContourIntegration/NumberedEquation10.gif" width=300 border=0>          

منابع:

Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 406-409, 1985.

Krantz, S. G. "Applications to the Calculation of Definite Integrals and Sums." §4.5 in Handbook of Complex Variables. Boston, MA: Birkh?user, pp. 51-63, 1999.

Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 353-356, 1953.

Whittaker, E. T. and Watson, G. N. "The Evaluation of Certain Types of Integrals Taken Between the Limits and ," "Certain Infinite Integrals Involving Sines and Cosines," and "Jordan"s Lemma." §6.22-6.222 in A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, pp. 113-117, 1990.